Y=4-x^2 parabola 960790-Y=x2-4x+2 parabola

 " " Given the Equation color(red)(y=f(x)=4x^2 A Quadratic Equation takes the form color(blue)(y=ax^2bxc Graph of a quadratic function forms a Parabola The coefficient of the color(red)(x^2 term (a) makes the parabola wider or narrow If the coefficient of the color(red)(x^2, term (a) is negative then the parabola opens down Let the focus and directrix of this particular parabola be Take a standard form of parabola equation ( x h) 2 = 4 p ( y k) In this equation, the focus is ( h, k p) Whereas the directrix is y = k p When at rest, the surface of mass of liquid is horizontal at PQ as shown in the figure A suitable rotation around the origin can thenOpens downward Move the y and 3 to the right, and then factor 2 out of the two x terms to get 2 ( x2 4 x) = – y 5 Complete the square in the parentheses, and add 8 to the right side Simplify and factor to get 2 ( x 2) 2 = –1 ( y – 5) Divide each side by 2

Solved Consider The Parabola Y 4x X2 A Find The Slope Chegg Com

Y=x2-4x+2 parabola

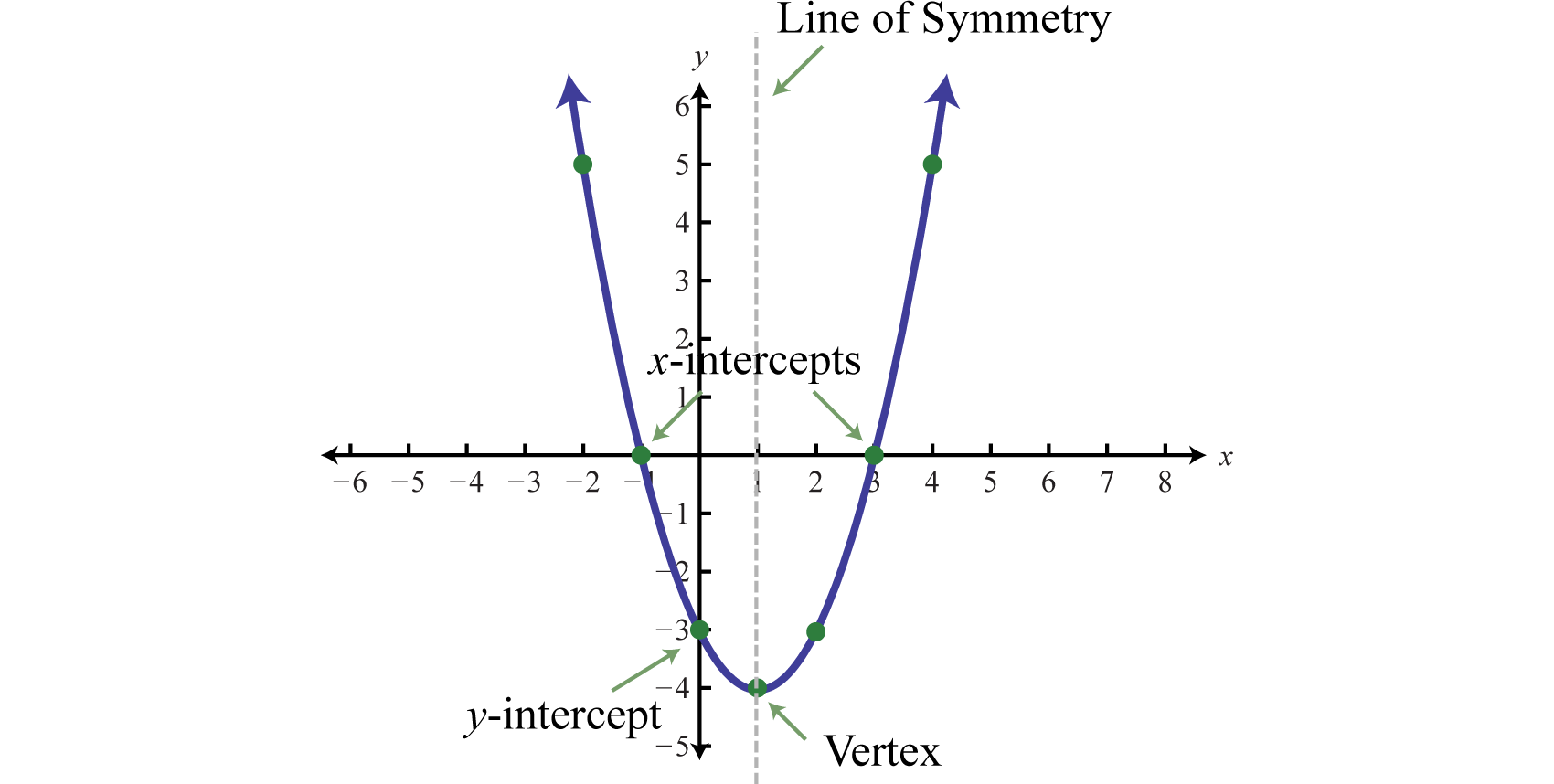
Y=x2-4x+2 parabola-Answer (1 of 9) Yes, its axis of symmetry is the xaxis If you have a quadratic equation in two unknowns, Ax^2BxyCy^2DxEyF=0 you can tell if the curve it represents is a parabola or not by its discriminant B^24AC If the discriminant is 0, it's a parabola;Since the parabola is symmetrical about the yaxis and has one root at , its other root is located at y = (x 2) (x 2) = 0 y = x^2 4 = 0 y = (1) (x^2 4) —— > y = x^2 4 (1)^2 4 = 1 4 = 3 (1)^2 4 = 1 4 = 3 So the equation of the parabola really is y = x^2 4

Solved Consider F And C Below F X Y X2 I Y2 J C Is Chegg Com

The vertex of a parabola represented by f(x)=x^24x3 has coordinates of (2,1) Find the coordinates of the vertex of the parabola defined by g(x)=f(x2) Explain how you arrived to your answer My question Would you move the algebra 2 The reflecting dish of a parabolic microphone has a crosssection in the shape of a parabola theThe equation of the parabola is y = 4 – x 2 ∴ x 2 = 4 – y, ie (x – 0) 2 = – (y – 4) It has vertex at P(0, 4) For points of intersection of the parabola with Xaxis, we put y = 0 in its equation ∴ 0 = 4 – x 2 ∴ x 2 = 4 ∴ x = ± 2 ∴ the parabola intersect the Xaxis at A (22 If the vertex of the parabola y = 4x² − 5x 10 is the point (h, k), what is the value of k?

And y = −√ x (the bottom half of the parabola) Here is the curve y 2 = x It passes through (0, 0) and also (4,2) and (4,−2) Notice that we get 2 values of y for each value of x larger than 0 This is not a function, it is called a relationFind the vertex of the parabola x = 0 y = 4 For a quadratic of the form ##x = ay^2 by c##, the axis is a line that passes through the vertex and is parallel to the ##y## axis For our parabola, the axis is the line y = 2 It's not part of the parabola itself, but lightly marking this line on your graph can help you see how the parabola curves symmetrically

If we take the value off excess zero, then why will be quarto zero square minus four So this will be quarto minus fourLet us now draw a perpendicular SZ from S to the directrix Then SZ will be the axis of the parabola Now, the midpoint of SZ ie A, will lie on P's locus ie AS=AZ The yaxis will be along the line AS, and the xaxis will be perpendicular to AS at A, as shown in the figure By definition PM = PS => MP 2 = PS 2 Ok so your original equation was y=4 (x2)²1 Therefore we need to expand the bracket to find the original equation To do this we need to find (x2)²=x²4x4 Now we multiply this by 4 and subtract 1 4x²16x15 Therefore B is the answer

Plot A Graph For The Equation Y X 2 4x

Quadratic Functions And Their Graphs

 The vertex form of the equation of a parabola is y = 4 (x 2)2 1What is the standard form of the Brainlycom brittanyspiresThis problem has been solved!If P is a point on the parabola y = x 24 which is closest to the straight line y =4 x 1, then the co ordinates of P are A 2,8B 1,5C 3,13D 2,8 Login Study Materials

How Do You Graph Y 4x 8 Socratic

Determine The Area Of The Region Bounded By The Parabola Y 4x 2 The Tangent Line To This Parabola At 2 16 And The X Axis Study Com

This second parabola y = x 2 V has the same shape as the original parabola y = x 2, but it is shifted V units up The graph of the quadratic function y = x 2 (blue curve) and y 5 (red curve), shifted up 5 units Here are the 3 possible cases for V (inThe area bounded by the parabola y=4−x 2 and X axis in sq units is The area bounded by the parabola y = 4So in this question, we have to plot the parable A Y is equal to X square minus for so like us First, find our bags and y coordinates for some points in orderto Lauretta parabola Draw two columns, one for export in it and one for Why coordinate now?

Quadratic Function

1

 Z = ∫ L ( x − y) d x x d y when L y = 4 − x 2, A ( 1;3), B ( 2; We actually have 2 functions, y = √ x (the top half of the parabola);

Solved An Equation Of A Parabola Is Given X 4 2 8 Y Chegg Com

Quadratics Graphing Parabolas Sparknotes

 The parabolas y^2 = 4x and x^2 = 4y divide the square region bounded by the lines x = 4, y = 4The equation of the other normal to the parabola $y^{2}=4 a x$ which passes through the point of intersection of normals at $(4 a,4 a) \&(9 a,6 a)$ is The answer is equation vertex (–2, 5);

Sketch The Region R That Lies Below The Parabola Y 4x X 2 Above The X Axis And Above The Line Y 3x 6 Find The Area Of The Region R Study Com

Solved Find The Vertex Focus And Directrix Of The Parabola Chegg Com

If positive, a hyper23 Determine the end behavior (a) f(x) = −4x5 6x³ 2x of the graph of each polynomial function given below (b) h(x) = 8x4 5x³ – 1 Question 22 If the vertex of the parabola y = 4x² − 5x 10 is the point (h, k), what is theAxis\(y3)^2=8(x5) directrix\(x3)^2=(y1) parabolaequationcalculator y=x^{2} en image/svgxml Related Symbolab blog posts Practice, practice, practice Math can be an intimidating subject Each new topic we learn has symbols and problems we have never seen The unknowing

Misc 15 Find Area X Y Y2 4x 4x2 4y2 9 Miscellaneous

Y X 3

 Harish Chandra Rajpoot Given equation of parabola y = (x 4)2 2 (x 4)2 = y −2 Comparing above equation with the standard form of vertical parabola (x −x1)2 = 4a(y − y1), we get x1 = −4,y1 = 2,a = 1 4 The vertex of above parabola is at (x1,y1) ≡ ( − 4,2) Axis of symmetry x −x1 = 0 Its form will be x = a( y – k) 2 h The parametric equations of a quadratic polynomial, parabola The parametric equations of the parabola, whose axis of symmetry is parallel to the yaxis The quadratic polynomial y = a 2 x 2 a 1 x a 0 or yy 0 = a 2 (xx 0) 2, V(x 0, y 0) You can take x= 1 and get the value for y PARABOLAS shapes areCompute properties of a parabola parabola with focus (3,4) and vertex (4,5) parabola (y2)^2=4x Compute the If the given equation is written in rectangular coordinate system, then we need to convert it into polar coordinate system as follows Next, substitute θ with θ ϕ and then expand using the sum and difference of two angles formula

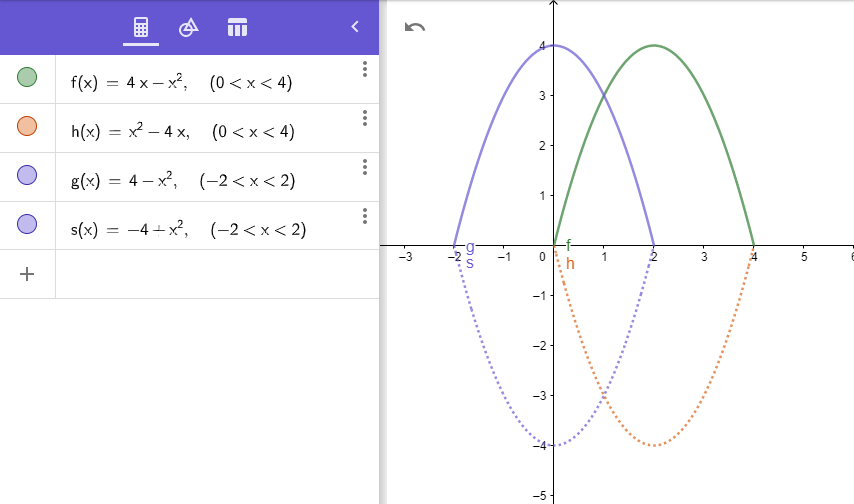
A Region Bounded By The Parabola Y 4x X And The X Axis Quizlet

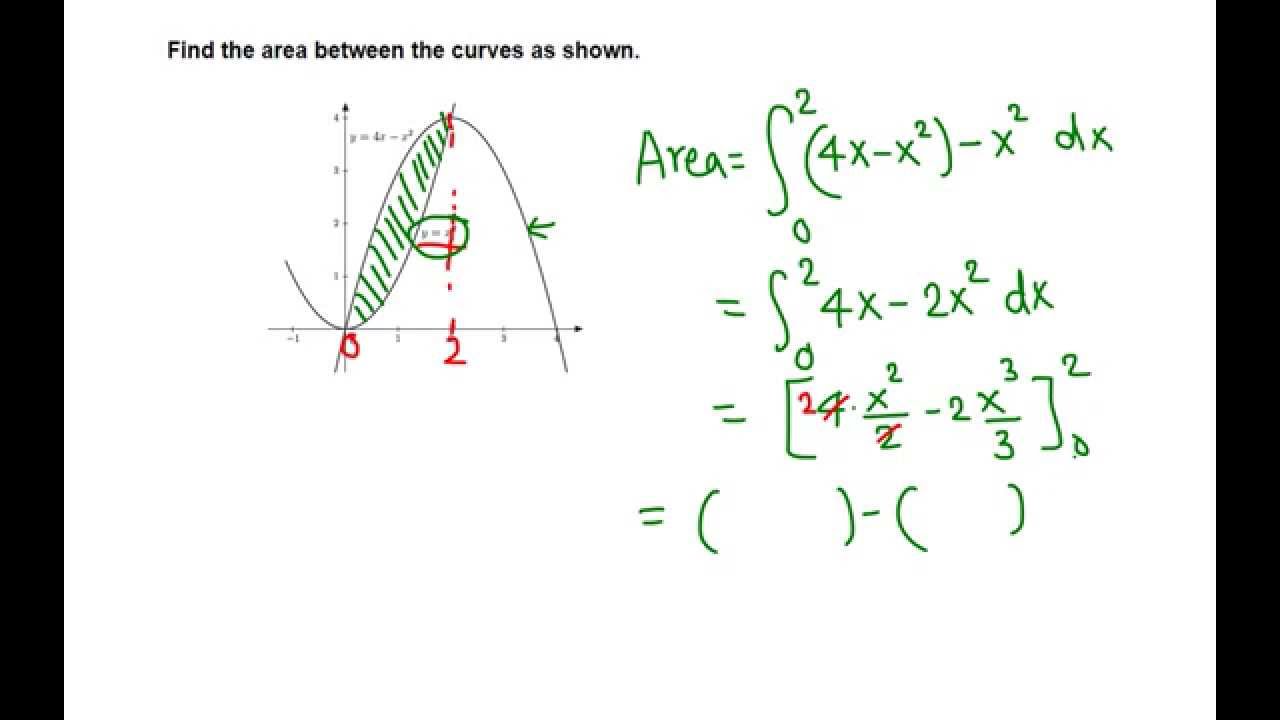
Area Between Y 4x X 2 And Y X 2 Youtube

SOLUTION Graph the parabola y = (x4)^2 2 Algebra > Quadratic Equations and Parabolas > SOLUTION Graph the parabola y = (x4)^2 2 Log On Quadratics solvers QuadraticsLet P be the point on the parabola y 2 = 4 x which is at the shortest distance from the center S of the circle x 2 y 2 − 4 x − 1 6 y 6 4 = 0 Let Q be the point on the circle dividing the line segment S P internally ThenThe focal length is found by equating the general expression for y `y=x^2/(4p)` and our particular example `y=x^2/2` So we have `x^2/(4p)=x^2/2` This gives `p = 05` So the focus will be at `(0, 05)` and the directrix is the line `y = 05` Our curve is as follows

Solved Consider The Parabola Y 4x X2 A Find The Slope Chegg Com

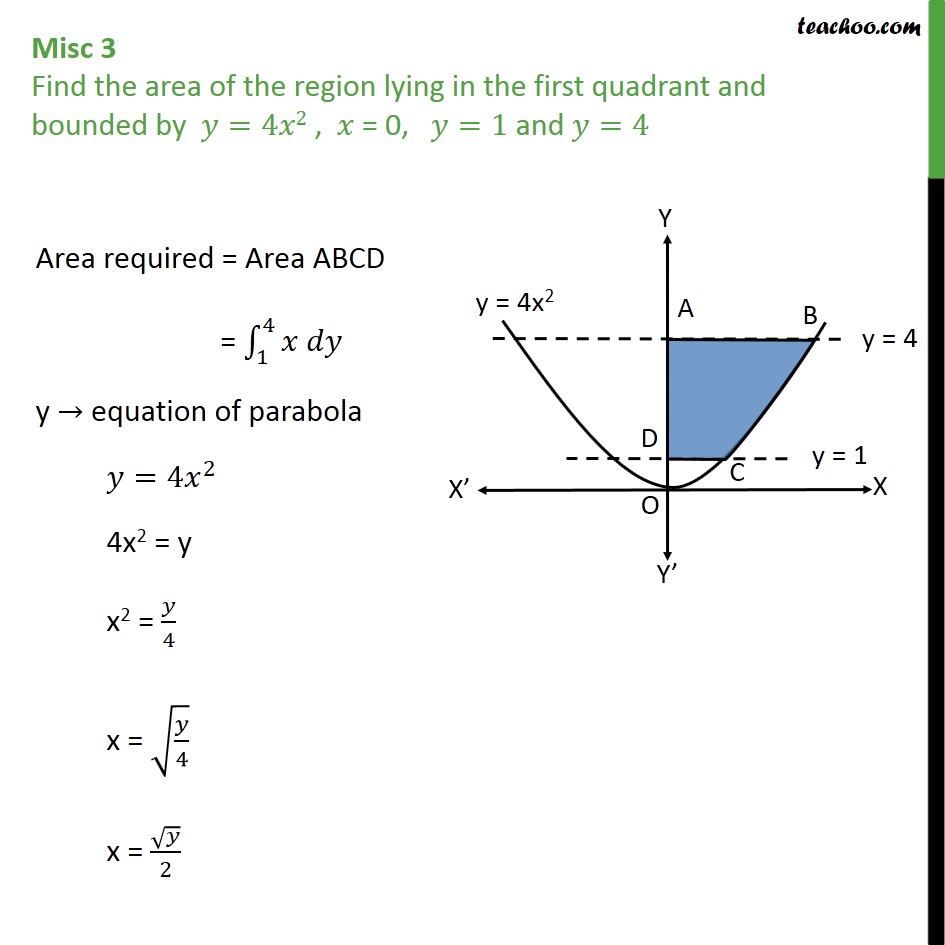
Misc 3 Find Area Bounded By Y 4x2 X 0 Y 1 Y 4

Parabola Equation The general equation of a parabola is y = a (xh) 2 k or x = a (yk) 2 h, where (h,k) denotes the vertex The standard equation of a regular parabola is y 2 = 4ax Some of the important terms below are helpful to understand the features and parts of a parabolaSo, the equation will be x 2 = 4ay Substituting (3, 4) in the above equation, (3) 2 = 4a(4) 9 = 16a a = 9/16 Hence, the equation of the parabola is x 2 = 4(9/16)y Or 4x 2 = 9y Go through the practice questions given below to get a thorough understanding of the different cases of parabolas explained above Practice Problems 1Free PreAlgebra, Algebra, Trigonometry, Calculus, Geometry, Statistics and Chemistry calculators stepbystep

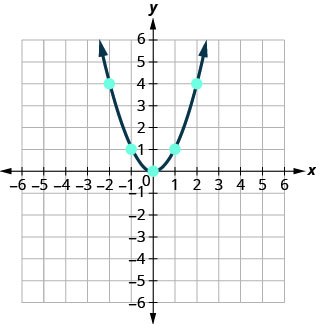
Graphing Quadratic Equations Elementary Algebra

What Is The Volume Of The Solid Bounded By The Parabola Y 4x 2 And The Lines X 0 And Y 16 By Revolving About The Line Y 2 Quora

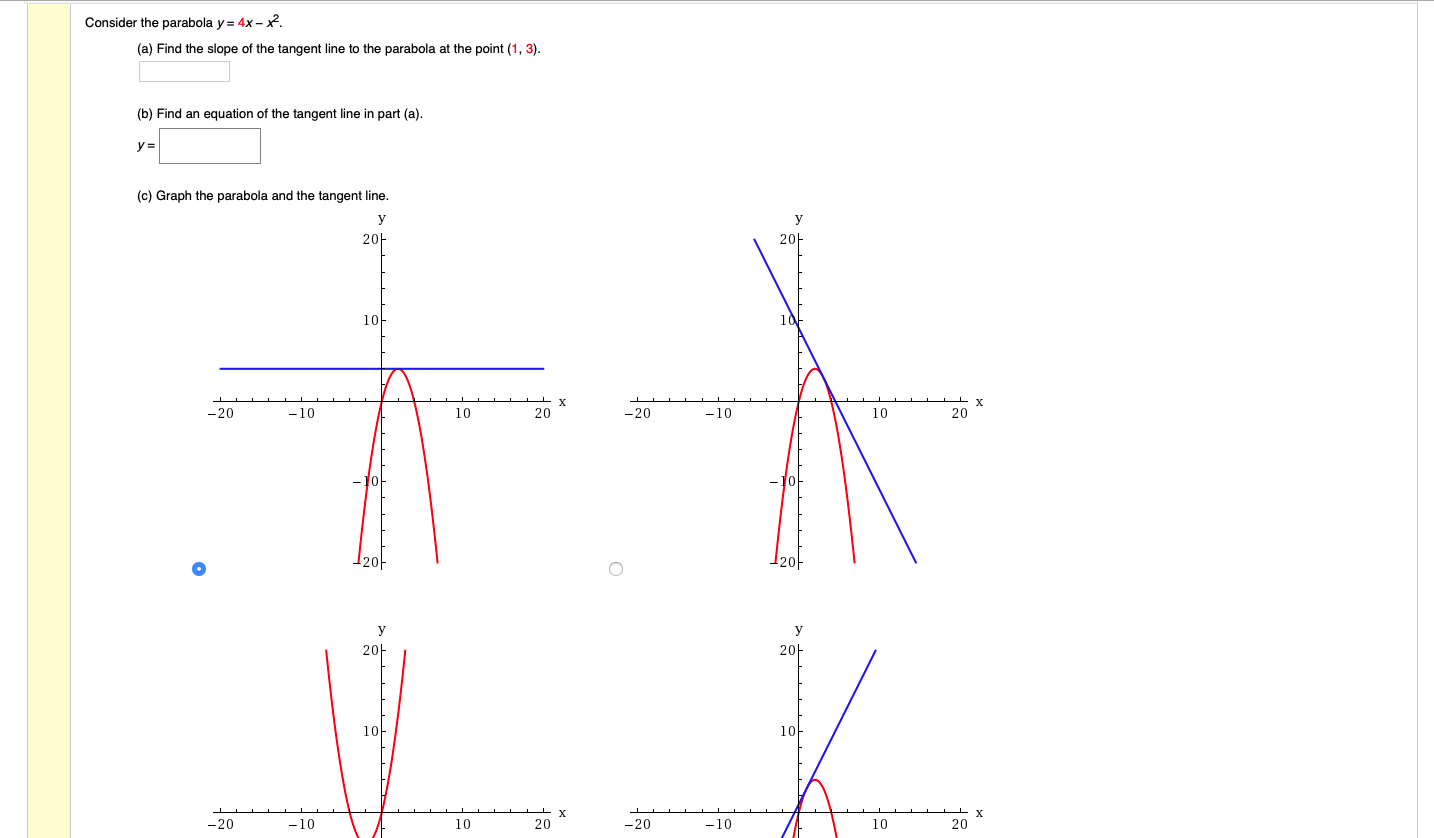
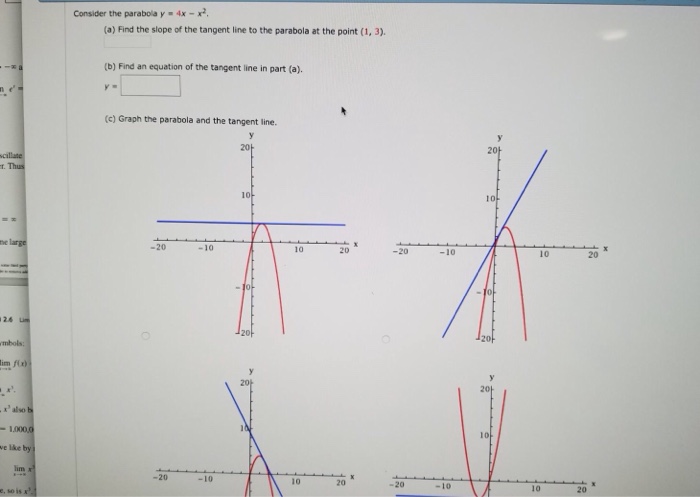
You can put this solution on YOUR website! Let's take a look at the first form of the parabola f (x) = a(x −h)2 k f ( x) = a ( x − h) 2 k There are two pieces of information about the parabola that we can instantly get from this function First, if a a is positive then the parabola will open up and if a a is negative then the parabola will open downSee the answer Consider the parabola y = 4 x − x2 (a) Find the slope of the tangent line to the parabola at the point (1, 3) (b) Find an equation of the tangent line in part (a) y = (c) Graph the parabola and the tangent line

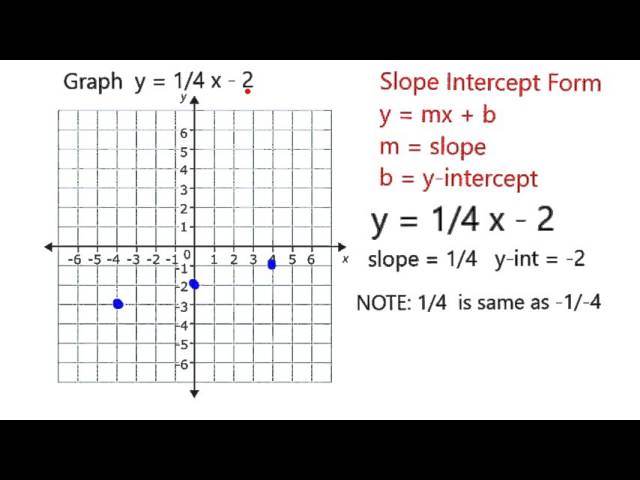
Graph Y 1 4 X 2 Youtube

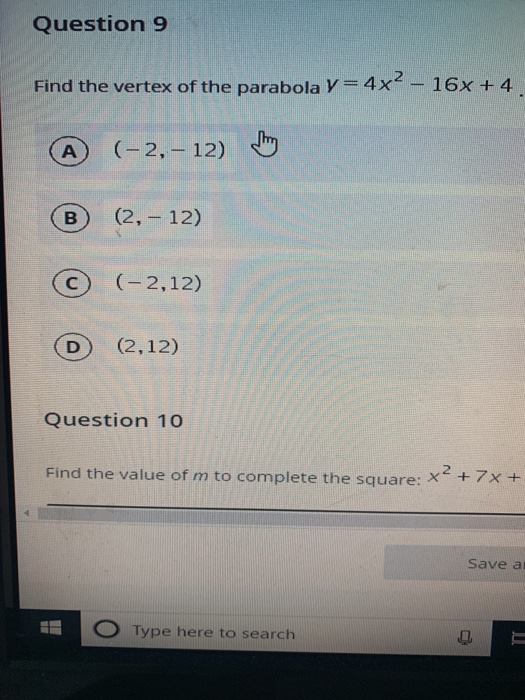
Solved Question 9 Find The Vertex Of The Parabola Y 4x2 Chegg Com

Solution (3) √2 / 3 x 2 = y 4, x 2 = 9 y Area bounded by the parabolas and y = 2 = 2 × ∫ 0 2 ( 3 y − y 2) d y = 5 ∫ 0 2 y d y = 5 × ( y) 3 / 2 3 / 2 = 10 3 × 2 2 = 2 3P(x,y) as any moving point;H = 5 ⋅ ( Z 0, 5) ⋅ 3 1 integration multivariablecalculus lineintegrals Share edited at 1314 user

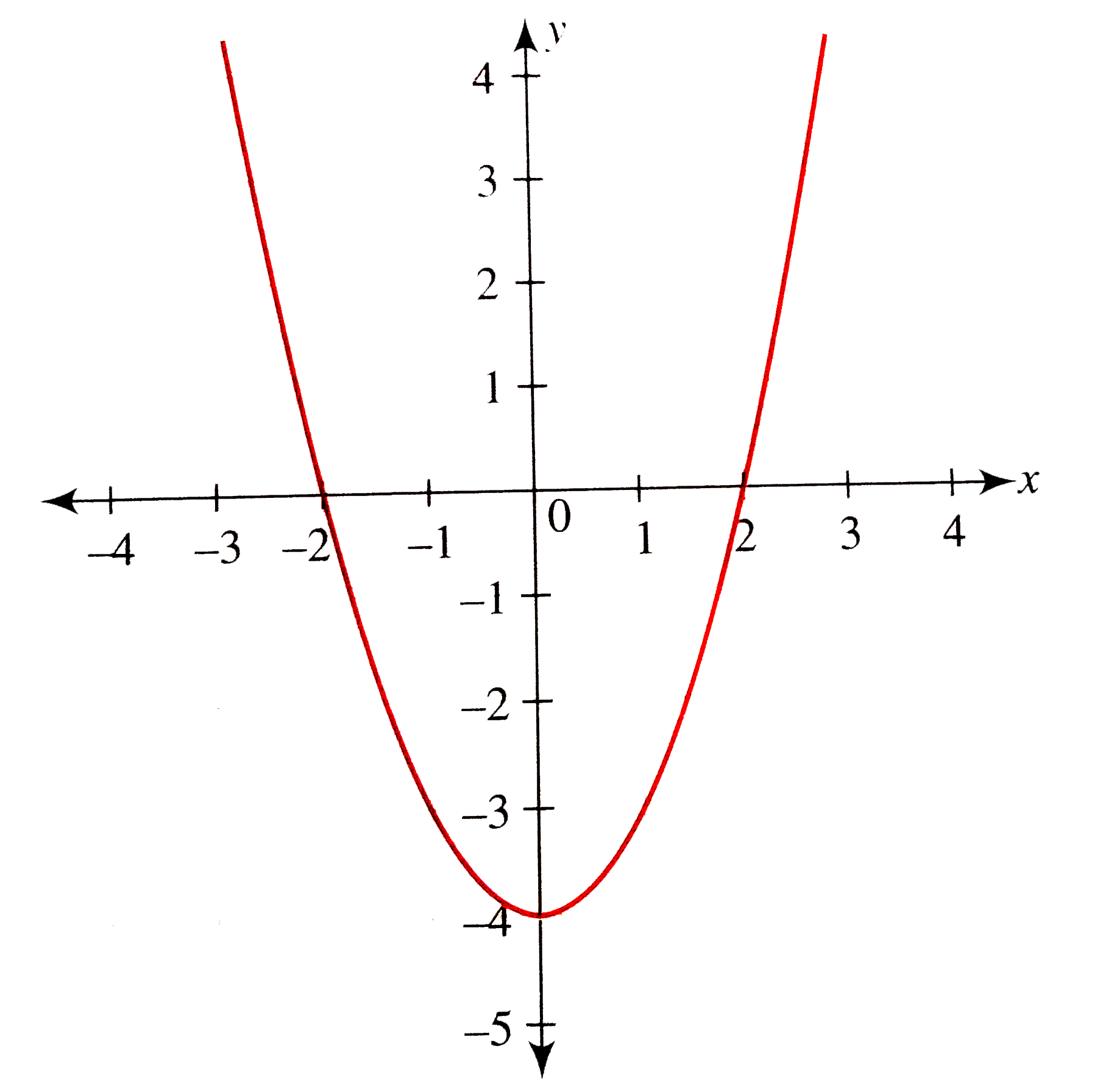
From The Graph Of Y X 2 4 Draw The Graph Of Y 1 X 2 4

Find The Centroid Of The Area Bounded By The Parabola Y 4 X 2 And The X Axis Study Com

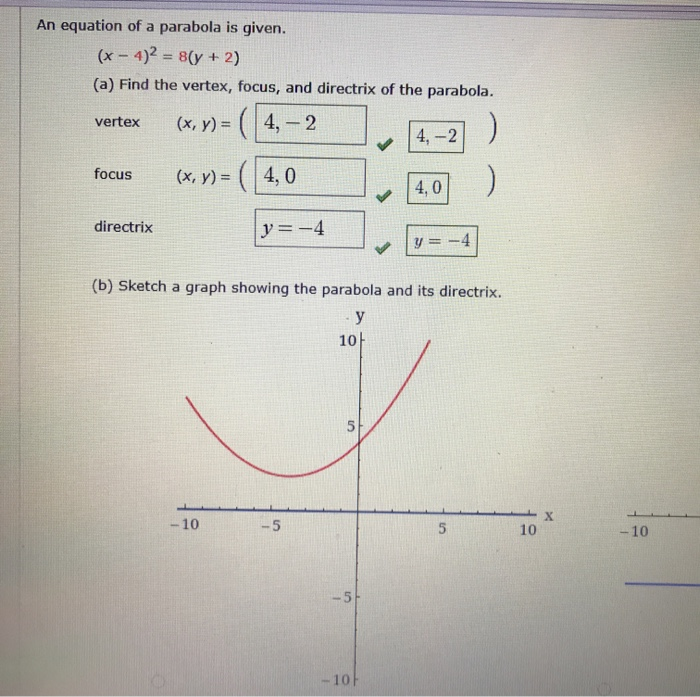
4 x 2 4 x 2 Set y y equal to the new right side y = 4 x 2 y = 4 x 2 y = 4 x 2 y = 4 x 2 Use the vertex form, y = a ( x − h) 2 k y = a ( x h) 2 k, to determine the values of a a, h h, and k k a = 4 a = 4 h = 0 h = 0 k = 0 k = 0 Since the value of a a is positive, the parabola opens upOn comparing the equation of the parabola y $^2$ = 12 x with the standard equation, y $^2$ = 4 ax, we get 4 a = 12 or a = 3 Hence, the focus, point C will be at (3, 0) and the extremities of the latusrectum AB will be at (a, 2a) and (a, 2a) So the coordinates of A and B are (3, 6) and (3,Parabola (x2)^2=8 (y4)

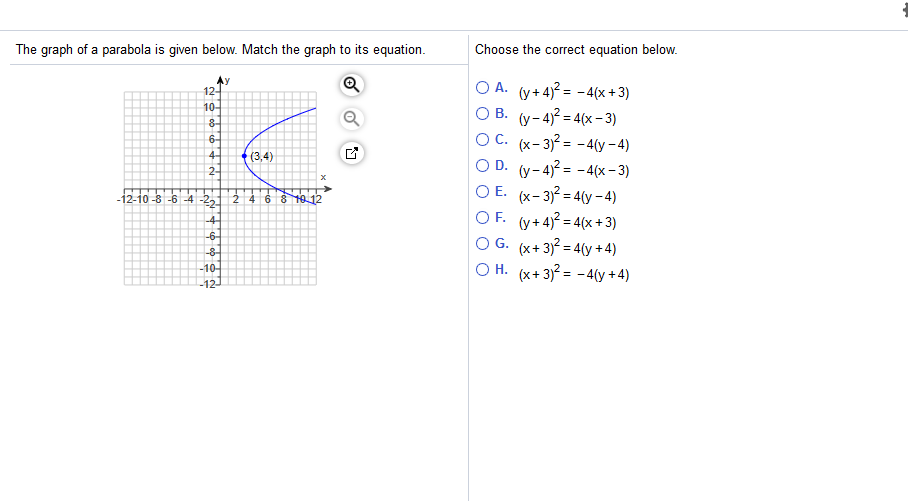
Solved Choose The Correct Equation Below The Graph Of A Chegg Com

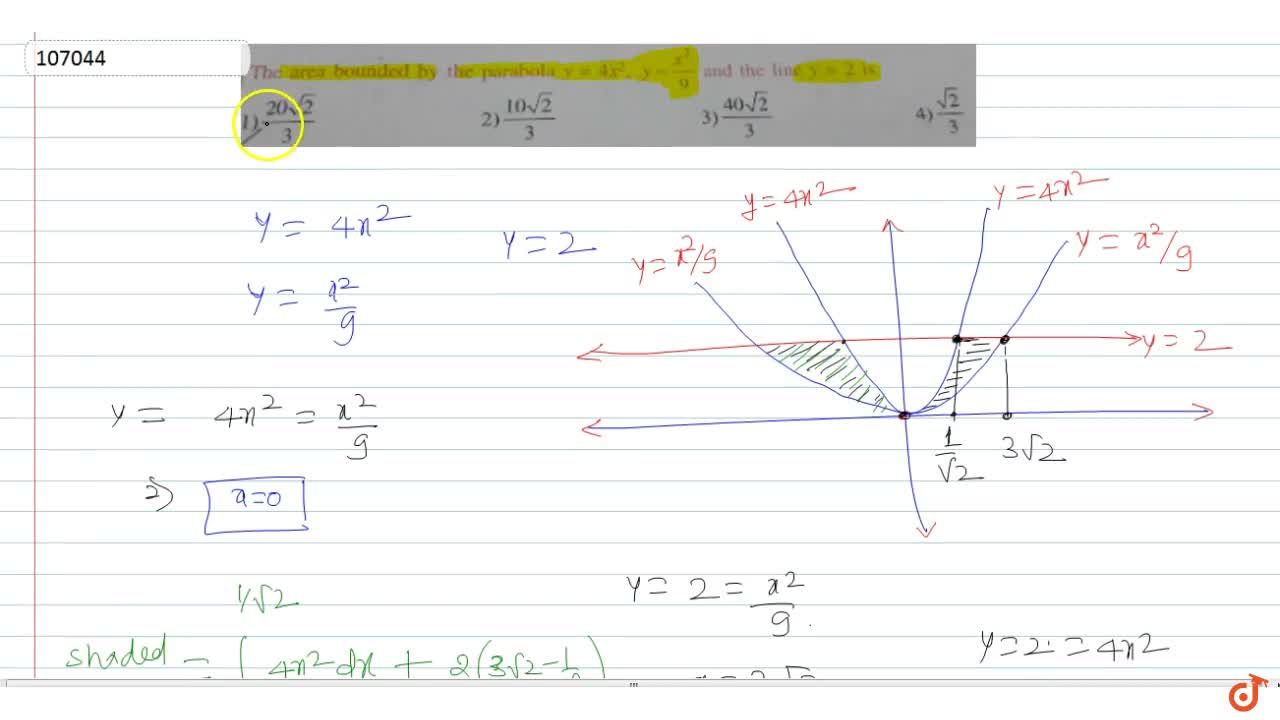
The Area Bounded By The Parabola Y 4x 2 Y X 2 9 And The Line Y 2 Is A sqrt2 3 B 10sqrt2 3 C 40sqrt2 3 D Sqrt2 3

 The parabolas y 2 = 4x and x 2 = 4y divide the square region bounded by the lines x = 4, y = 4 and the coordinate axes If S 1, S 2 and S 3 are respectively the areas of these parts numbered from top to bottom, then S 1 S 2 S 3 is equal to (a) 13) parabola y= 2(x3)^24 ma dwa punkty wspolne z prostą o rownaniu a) y=0 b) y=4 c) y=6 d) y=10 Nauka w grupie może być fajna! This question is from George Simmons' Calc with Analytic Geometry This is how I solved it, but I can't find the two points that satisfy this

How Do You Graph Y 4 X 2 2 1 Socratic

How To Show That Line Y 3 Meets Parabola Y 4 X 2 At D 1 3 And E 1 3 Quora

Write the equation of parabola in standard form y 2 8y = x 19 y 2 2(y)(4) 4 2 4 2 = x 19 (y 4) 2 4 2 = x 19 (y 4) 2 16 = x 19 Add 16 to each side (y 4) 2 = (x 3) (y 4) 2 = (x 3) is in the form of (y k) 2 = 4a(x h) So, the parabola opens up and symmetric about xaxis with vertex at (h, k) = (3, 4)The axis of symmetry is located at y = k Vertex form of a parabola The vertex form of a parabola is another form of the quadratic function f(x) = ax 2 bx c The vertex form of a parabola is f(x) = a(x h) 2 k The a in the vertex form of a parabola corresponds to the a in standard form If a is positive, the parabola will open upwardsThe simplest equation for a parabola is y = x 2 Turned on its side it becomes y 2 = x (or y = √x for just the top half) A little more generally Find the focus for the equation y 2 =5x Converting y 2 = 5x to y 2 = 4ax form, we get y 2 = 4 (5/4) x, so a = 5/4, and the focus of y 2 =5x is F = (a, 0) = (5/4, 0) The equations of parabolas

Solved Consider F And C Below F X Y X2 I Y2 J C Is Chegg Com

Solved Consider The Parabola Y 4x X2 A Find The Slope Chegg Com

Graphing Quadratic Functions

1

Solution Find The Vertex Of The Parabola Y 4x2 16x 11

Solution What Is The Vertex Of The Parabola Y 4x 2 8x 3 What Is A Parabola

Ch 4 Pre Test 1 Graph The Function Y 4x 2 Then Label The Vertex And Axis Of Symmetry 2 Write The Quadratic Function In Standard Form Y X Ppt Download

Solved Graph The Parabola Y 4x 2 4x A What Is Y Chegg Com

Graphing Quadratic Functions

Graph Quadratic Functions Using Properties Intermediate Algebra

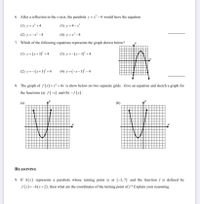
Answered 6 After A Reflection In The X Axis Bartleby

Solution Graph The Parabola Y X2 4x 4 Use The Quadratic Formula To Solve The Equation To The Exact Value Or Round To Two Decimal Places 2x 2 X 1

Exploration Of Parabolas

Find The Equation Of The Tangent To The Parabola Y 2 4x 5 Which Is Parallel To The Strai Youtube

How To Find Quadratic Line Of Symmetry

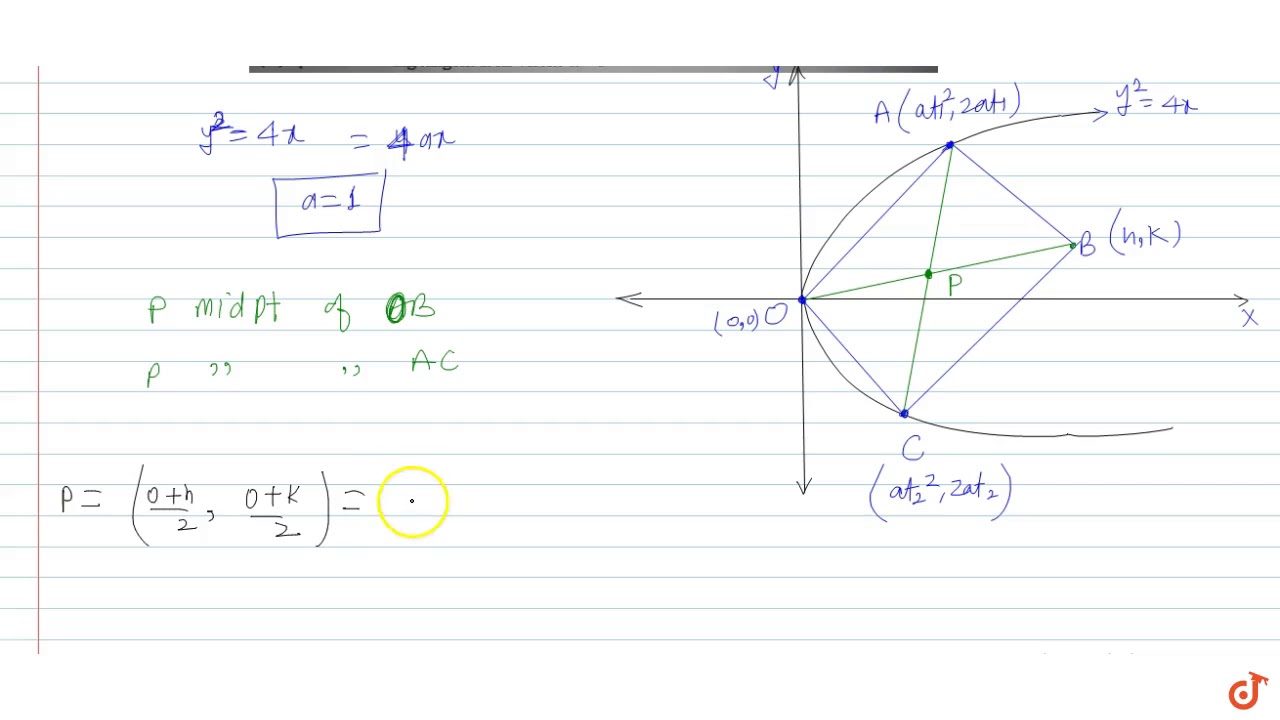
If From The Vertex Of A Parabola Y 2 4x A Pair Of Chords Be Drawn At Right Angles To One An Youtube

Where Do Y X 2 4x 1 And Y 3 X Intersect Mathskey Com

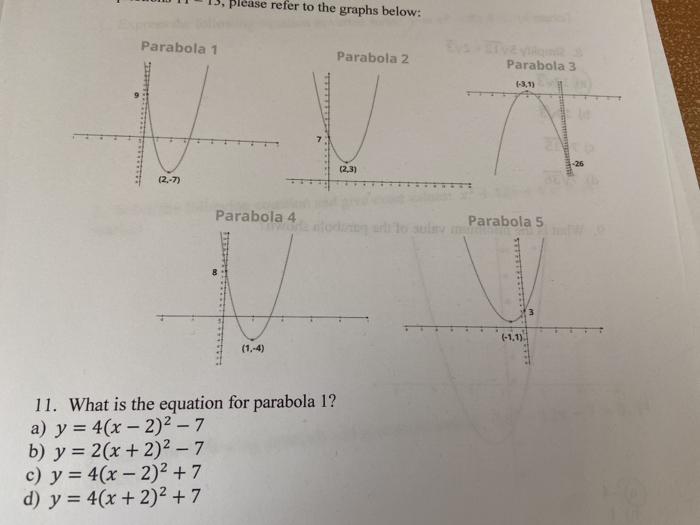
Solved Please Refer To The Graphs Below Parabola 1 Parabola Chegg Com

Math Lesson 7

Solved Example 1 Find An Equation Of The Tangent Line To The Chegg Com

The Parabola Given By Y 4x2 1 And The Line Given B Gauthmath

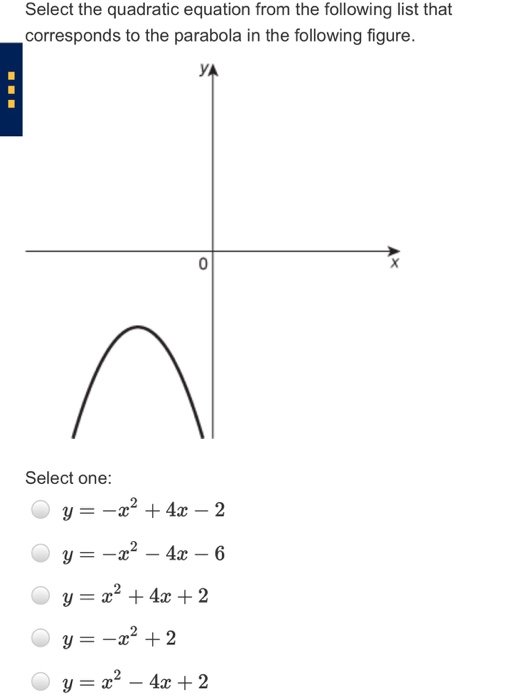
Solved Select The Quadratic Equation From The Following List Chegg Com

Characteristics Of Parabolas College Algebra

8 Consider The Parabola Whose Equation Is Y X2 4x Gauthmath

Ex 8 2 7 Mcq Area Lying Between Y2 4x And Y 2x Is

The Parabola Y 2 4x And X 2 4y Divide The Square Region Bounded By The Lines X 4 Y 4 And The Coordinate Axes If S1 S2 And S3

Untitled Document

The Equation Of The Directrix Of The Parabola Y 2 4y 4x 2 0 Is X 1 B X 1 X 3 2 D Youtube

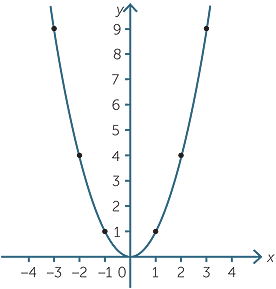
Quadratic Function

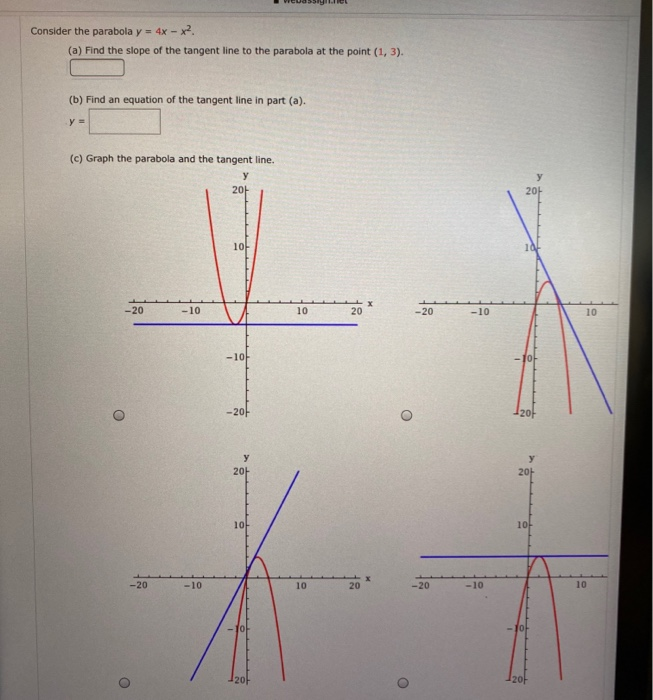
Solved Consider The Parabola Y 4x X2 A Find The Slope Chegg Com

Solved Example 2 The Arc Of The Parabola Y 4x2 From 1 4 Chegg Com

Find The Area Of The Region Bounded By The Parabola Y 4x 2 The Tangent Line To This Parabola At 4 64 And The X Axis Study Com

How Do You Graph Y X 4 2 Socratic

Solution Graph The Following Parabola X 4 2 4 Y 1

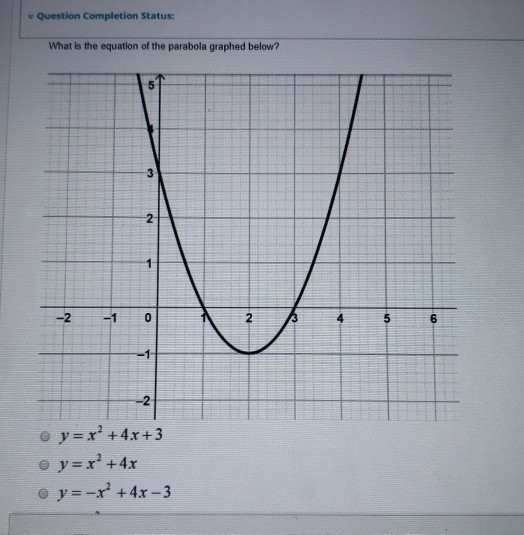
Solved Question Completion Status What Is The Equation Of Chegg Com

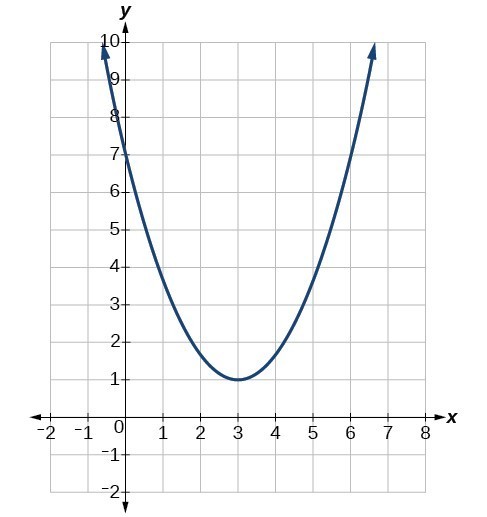
Characteristics Of Parabolas College Algebra

Quadratics Graphing Parabolas Sparknotes

The Region Bounded Below By The Parabola Y X 2 And Above By The Line Y 4 Is To Be Partitioned Into Two Subsections Of Equal Area By Cutting Across It

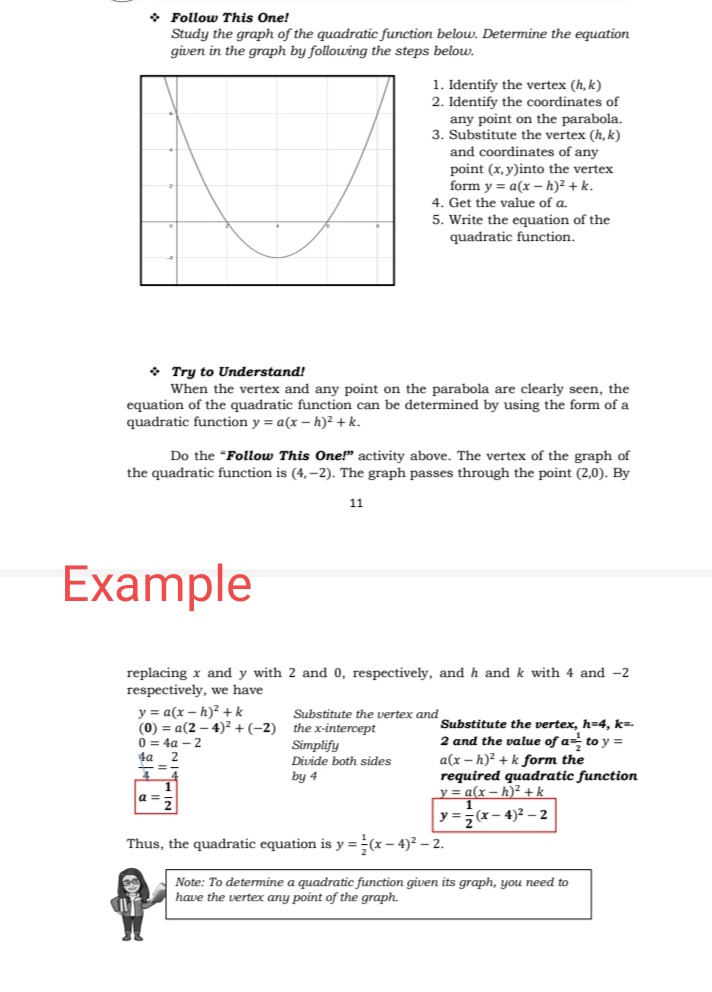
Answered A Y X 2 B Y X 2 C Y X Bartleby

Quadratic Function

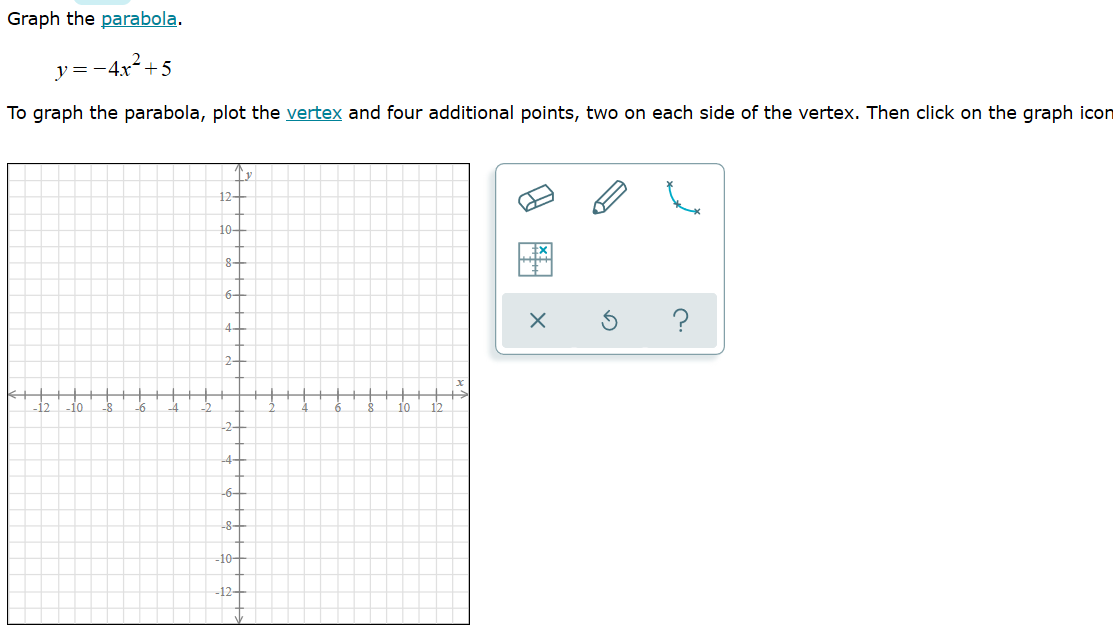
Solved Graph The Parabola Y 4 X2 5 To Graph The Parabola Chegg Com

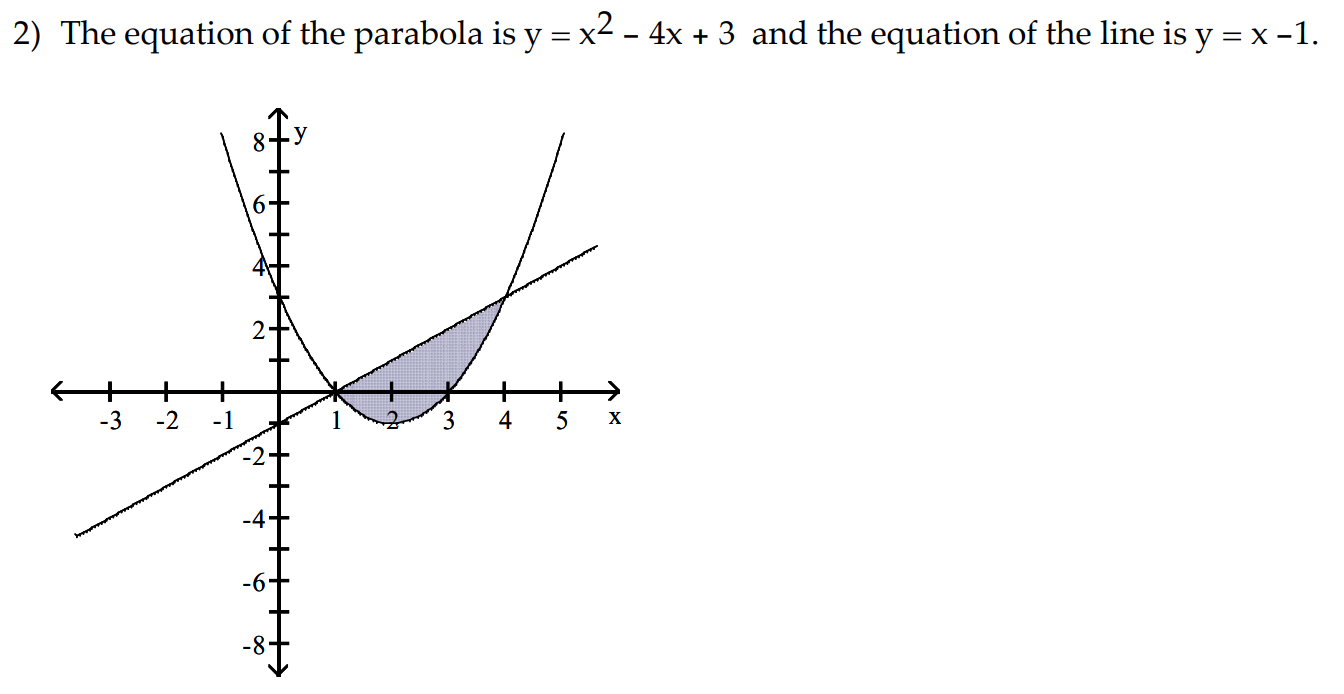
Solved 2 The Equation Of The Parabola Is Y X2 4x 3 Chegg Com

The Region Bounded By The Parabola Y 4 X And The Line Y 2 X Is Revolved About The X Axis To Generate A Solid I Give A Sketch

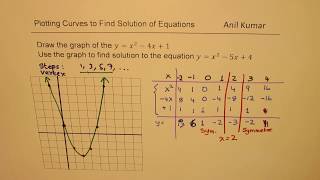
Step To Draw Y X 2 4x 1and Find Solution To Quadratic Equation Y X 2 5x 4 Youtube

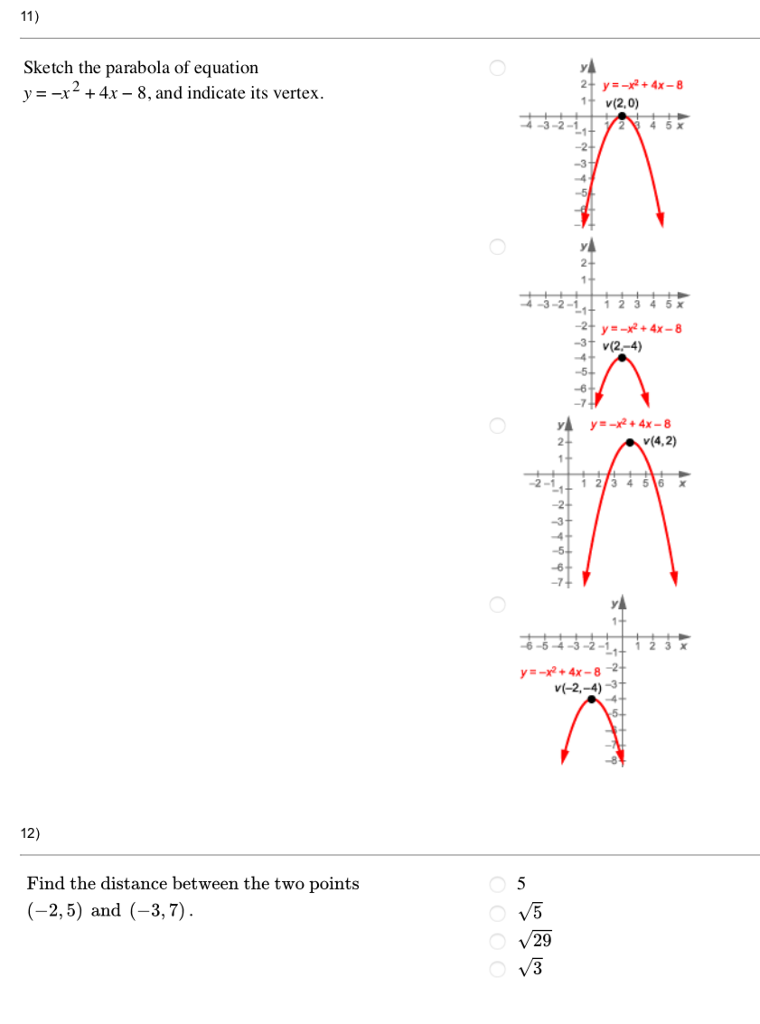
Solved 11 Sketch The Parabola Of Equation Y X 4x 8 And Chegg Com

Solved What Point On The Parabola Y 4 X2 Is Closest To Chegg Com

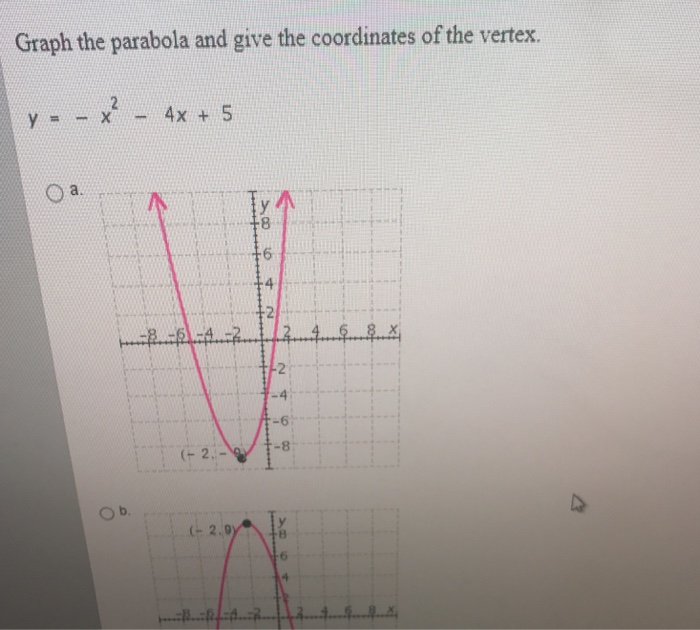
Solved Graph The Parabola And Give The Coordinates Of The Chegg Com

The Equation Of The Directrix Of The Parabola Y 2 4y 4x 2 0 Is X 1 B X 1 X 3 2 Youtube

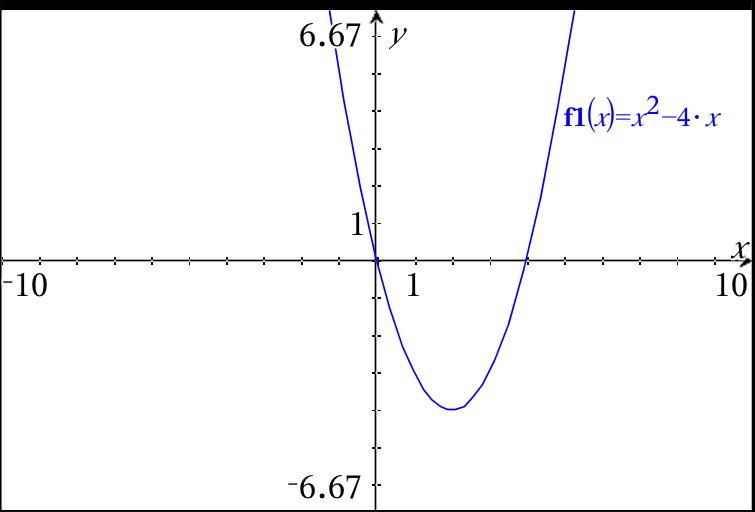
What Is The Graph Of F X X 2 4x Socratic

What Is The Area Of The Region Bounded By The Parabola Y 2 4x And The Line X 1 Quora

Graphing Quadratic Functions

Exploration Of Parabolas

How To Graph A Parabola Of The Form Y X 2 Bx C Algebra Study Com

Solution Graph The Parabola Y 5 4x 2 To Graph The Parabola Plot The Vertex And Four Additional Points Two On Each Side Of The Vertex Then Click On The Graph Icon

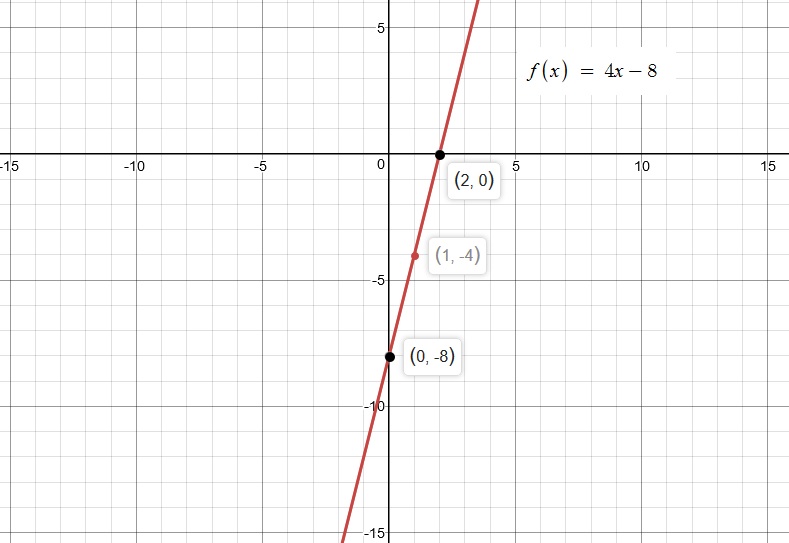
How To Graph Y 4x 1 Quora

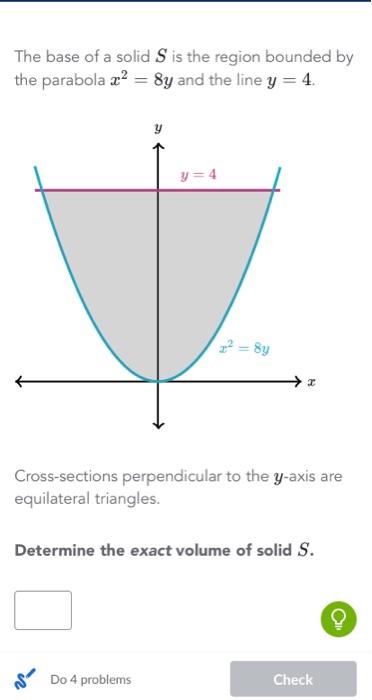
Solved The Base Of A Solid S Is The Region Bounded By The Chegg Com

2 Y 2x2 10 With Parabola Y 4x 16 X 2 And Chegg Com

Consider The Parabola Y 4x X2 A Find The Slope Of Gauthmath

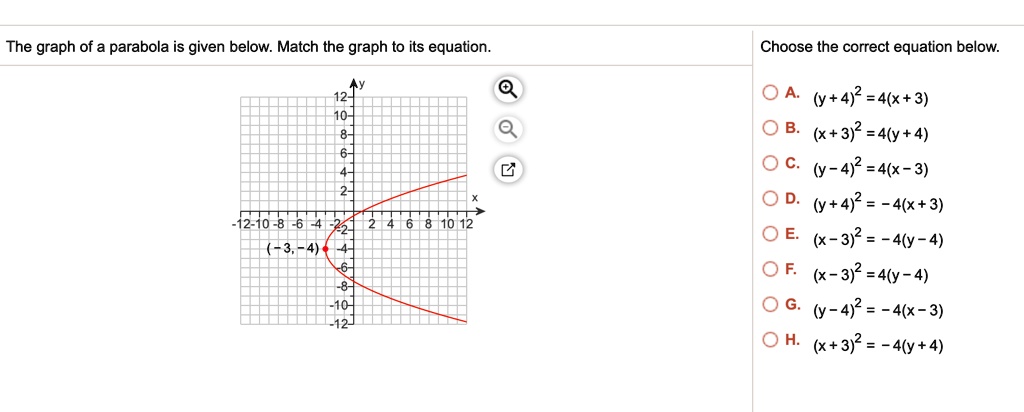
Solved The Graph Of A Parabola Is Given Below Match The Graph To Its Equation Choose The Correct Equation Below 0a Y 4 2 4 X 3 X 3 2 4 Y 4 Y 4 2 4 X 3 Y 4 2 4 X 3 X 3 2

Exploration Of Parabolas

Graph Quadratic Functions Using Properties Intermediate Algebra

Parabolas

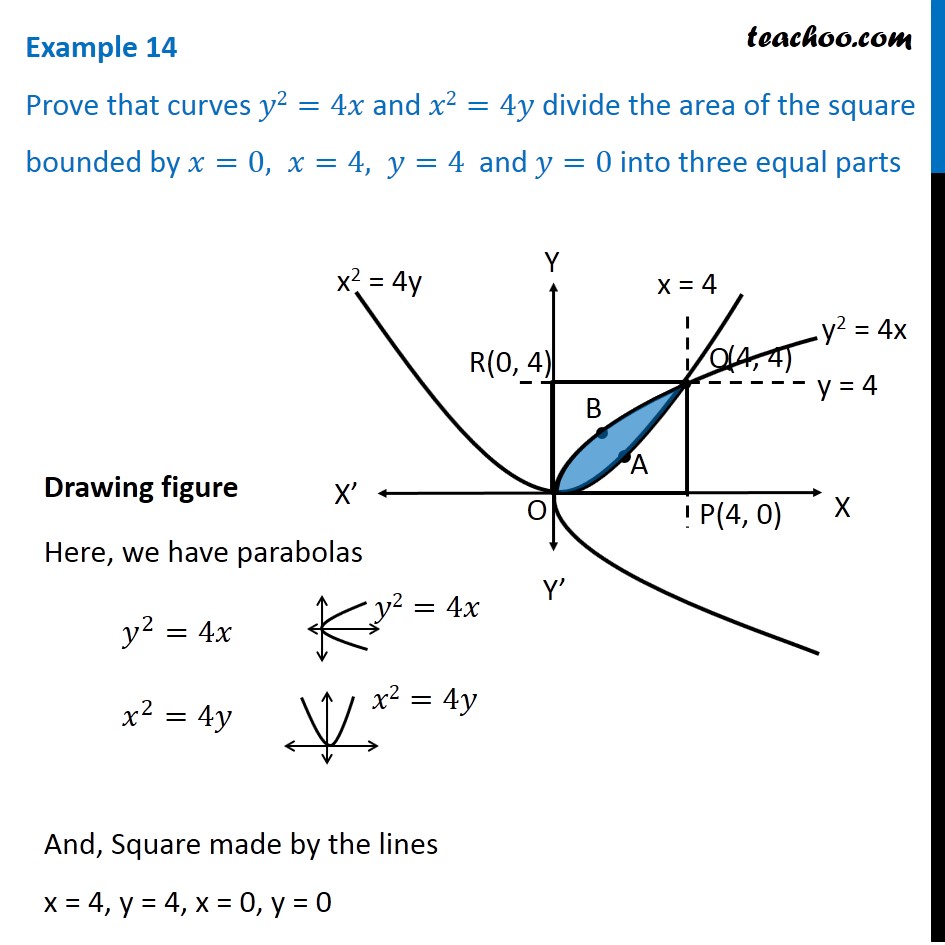
Example 14 Prove That Y2 4x X2 4y Divide Area Of Square

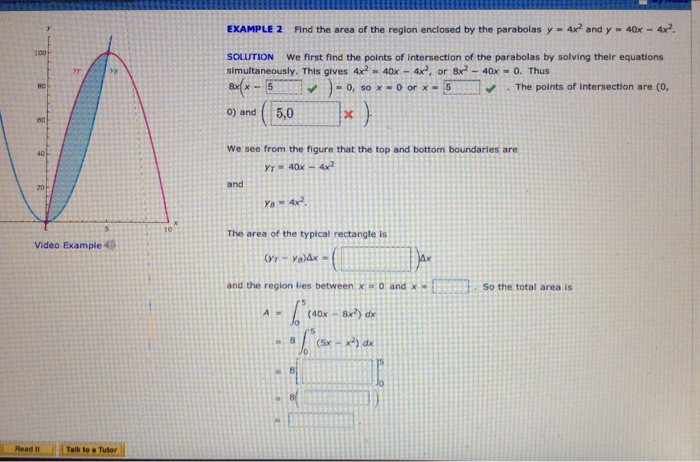
Solved Find The Area Of The Region Enclosed By The Parabolas Chegg Com

Solved Consider The Quadratic Function Y X 2 4x 1 Chegg Com

Let A Be The Vertex And L The Length Of The Latus Rectum Of The Parabola Y 2 2 Y 4x Youtube

How To Represent The Graph Of The Parabola Y 2 4x Quora

Find The Area Of The Region Bounded By The Parabola Y X 2 And The Line Y 4 Study Com

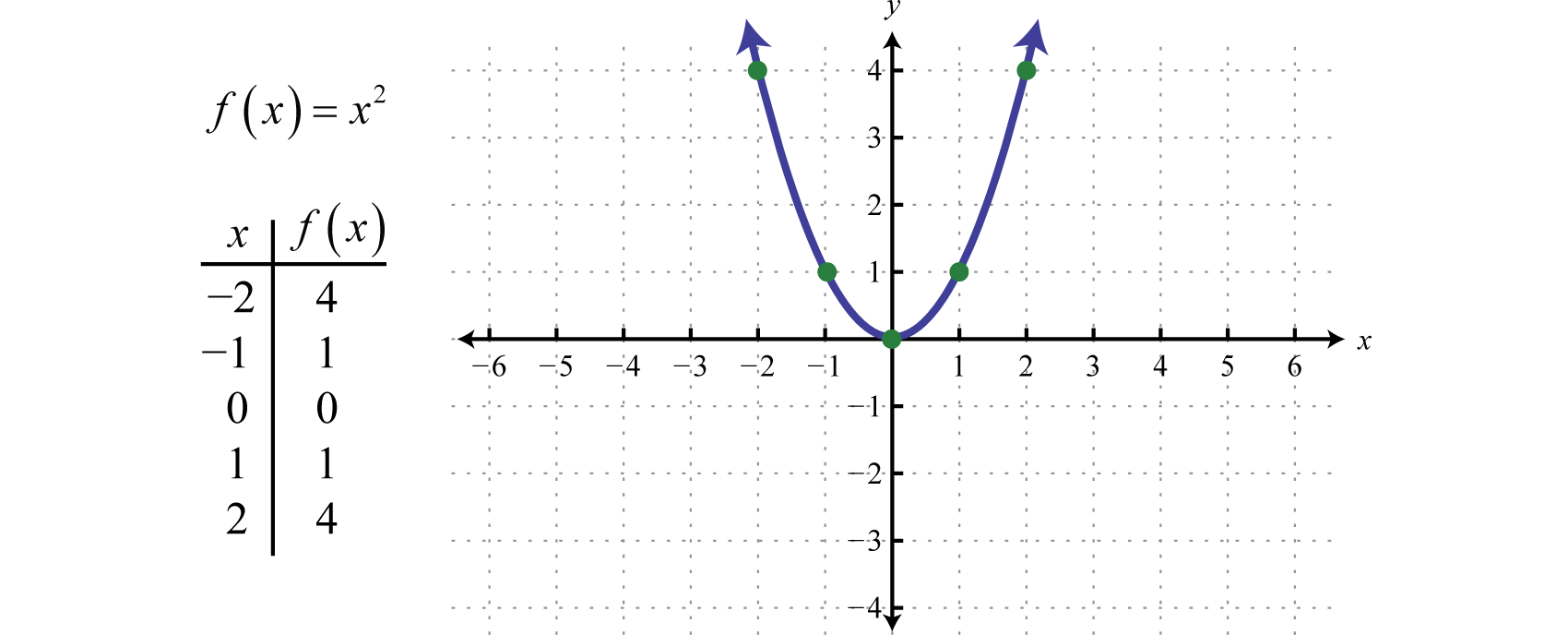
Quadratic Functions And Their Graphs

Parabola Parent Function Mathbitsnotebook A1 Ccss Math

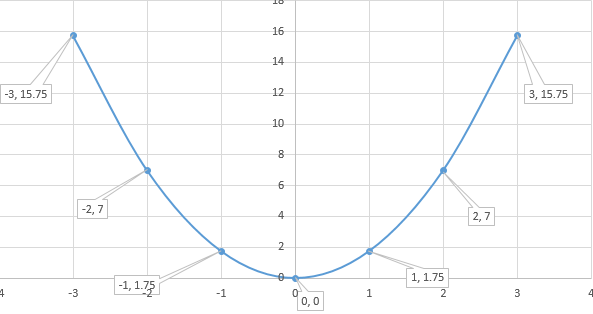
How Do You Graph The Parabola Y 7 4x 2 Using Vertex Intercepts And Additional Points Socratic

Incoming Term: y=4-x^2 parabola, y=4-x^2 graph, y=x^2 parabola, y=x^2-2x-4 parabola, y=x2-4x+2 parabola, y+4=-3(x+2) graph, y+5=4(x+2) graph, y=x^4-4x^2 graph, y=f(x-4)+2 graph, y-4=1/3(x-2) graph,